
Unit 5 - Linear Functions

Statement of Inquiry
Models are depictions of real-life events using expressions, equations or graphs while a function is defined as a relation or expression involving one or more variable. Creating different representations of functions to model the relationships between variables, visually and symbolically as graphs, equations and/or tables represents different ways to communicate mathematical ideas.
Concepts
Change,
Modelling
Change:
A variation in size, amount, or behavior. READ MORE >>
Modelling:
Depictions of real-life events using expressions, equations, or graphs. READ MORE >>
Learning Topics
Course Syllabus Topics
-
Function
-
Domain and range
-
Graphing functions
-
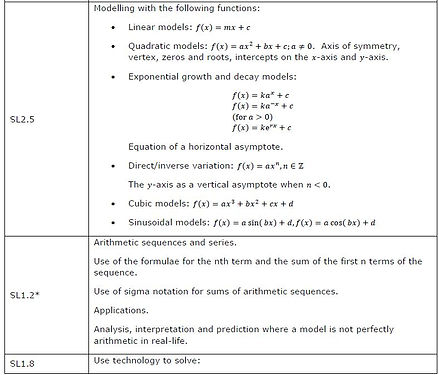
Linear models and their parameters
-
Rate of change
-
Direct variation
-
Inverse function
-
Arithmetic sequences and series
-
Common difference
-
General term
-
Sum of Series
-
Simple interest
-
Prediction
-
Extrapolation vs interpolation
Prior Learning Support
Prior Learning 1: Solving Linear Equations
Prior Learning 2: Solving Linear Inequalities
Prior Learning 3: Graphing Linear Functions

Conceptual Understandings
-
Different representations of functions, symbolically and visually as graphs, equations, and tables provide different ways to communicate mathematical relationships
-
The parameters in a function or equation may correspond to notable geometrical features of a graph and can represent physical quantities in spatial dimensions
-
Moving between different forms to represent functions allows for deeper understanding and provides different approaches to problem solving
-
Our spatial frame of reference affects the visible part of a function and by changing this "window" we can show more or less of a function to suit our needs
-
Modelling real-life situations with the structure of arithmetic and geometric sequences and series allows for prediction, analysis and interpretation
-
Modelling and finding structure in seemingly random events facilitates prediction
Further Conceptual Understandings

Lesson 1:
Functions, Domain and Range, and Function Notation

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
j
Reflect
Lesson 2:
Linear Models and
Inverse Functions

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 3:
Arithmetic
Sequences

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 4:
Sums of Series
and Sigma Notation

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 5:
Simple Interest
and Modelling

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 6:
Unit Review

Get a start on the
Unit Review in the
Collaborate section...
Ask your questions
in our Unit Discussion.
Learn

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?

