
Unit 4 - Coordinate Geometry

Statement of Inquiry
Models are depictions of real-life events using expressions, equations or graphs while a function is defined as a relation or expression involving one or more variable. Creating different representations of functions to model the relationships between variables, visually and symbolically as graphs, equations and/or tables represents different ways to communicate mathematical ideas.
Geometry allows us to quantify the physical world, enhancing our spatial awareness in two and three dimensions. This branch provides us with the tools for analysis, measurement and transformation of quantities, movements, and relationships.
Concepts
Space,
Relationships
Space:
The frame of geometrical dimensions describing an entity. READ MORE >
Relationships: the connections and associations between properties, objects, people, and ideas -- including the human community's connections with the world in which we live. READ MORE >
Learning Topics
-
Gradient
-
Equations of straight lines
-
Perpendicular lines
-
Parallel lines
-
Perpendicular bisectors
-
Points of intersections of lines
-
Coordinates of midpoint and distance in 3D
-
Voronoi diagrams
-
Area of Voronoi diagrams
Prior Learning Support
Prior Learning Topic 1 - Solving Linear Equations
Prior Learning Topic 2 - Coordinates
Prior Learning Topic 3 - Pythagoras' Theorem
Prior Learning Topic 4 - Substituting into Formulae
Course Syllabus Topics


Conceptual Understandings
-
The parameters in a function or equation may correspond to notable geometric features of a graph and can represent physical quantities in spatial dimensions
-
Systems of equations often, but not always, lead to intersection points
-
In two dimensions, the Voronoi diagram allows us to navigate, path-find or establish an optimum position.
Further Conceptual Understandings
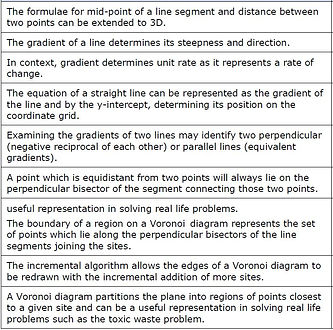
Lesson 1:
Midpoint and
Distance Formulas
Link to the Course Calendar

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 2:
Gradient of a Line
and Unit Rates

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 3:
Forms of
Linear Equations

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 4:
Parallel and
Perpendicular Lines

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Why have mathematics and statistics sometimes
been treated as separate subjects?
Reflect
Lesson 5:
Voronoi Diagrams

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
None today.
Reflect
Lesson 6:
Unit Review

Get a start on the
Unit Review
assignment...
Ask your questions
in our Unit Discussion.
Learn

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
None today.

