
Units 5 - Differential Calculus

Statement of Inquiry
Calculus describes rates of change between two variables. Understanding these rates of change allows us to model, interpret, and analyze real-world problems and situations. Calculus helps us understand the behavior of functions and allows us to interpret the features of graphs.
Concepts
Change,
Relationships
Change: a variation in size, amount or behavior. READ MORE >
Relationships: the connections and associations between properties, objects, people, and ideas -- including the human community's connections with the world in which we live. READ MORE >
Learning Topics
-
Limit of a function at a point
-
Derivative function as the gradient
of a curve, and as a rate of change -
The power rule for differentiating
polynomial functions -
Tangents and normals to curves
-
Differentiation rules: chain, product, quotient
-
Maxima, minima, and points of inflexion
-
Kinematics problems
-
Optimization
Prior Learning Support
Prior Learning 1 - Finding Gradients of Lines
Prior Learning 2 - Graphing Functions
Prior Learning 3 - Sequences
Course Syllabus Topics

Conceptual Understandings
-
The derivative may be represented physically as a rate of change and geometrically as the gradient or slope function
-
Examining rates of change close to turning points helps you identify intervals where the function increases/decreases, and identify concavity of the function
-
Mathematical modeling can provide effective solutions to real-life problems in optimization by maximising or minimising a quantity, such as cost or profit
-
Derivatives and integrals describe real-world kinematics problems in two and three dimensional space by examining displacement, velocity, and acceleration
Unit Discussion
Questions & Suggestions
Click on the microphone icon to enter our
Unit and Lesson Discussion.
-
Begin a discussion thread by adding a specific
question under a Lesson heading. -
Suggest links to videos and websites that have
helped you in your learning.
Further Conceptual Understandings
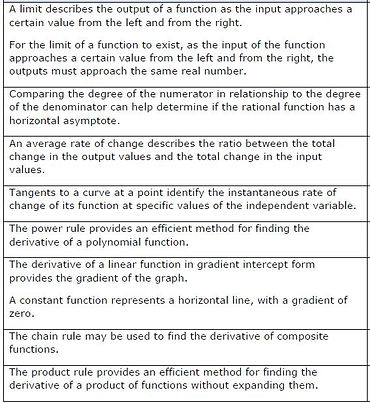
Lesson 1:
Limits

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 2:
Basic Derivative
Rules

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 3:
Tangent and
Normal Lines

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 4:
The Chain Rule

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 5:
Product and
Quotient Rules

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 6:
First Derivative
Test

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 7:
Graphing
Derivatives


In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 8:
Second Derivative Test & Concavity

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 9:
Optimization

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 10:
Kinematics

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Reflect
Lesson 11:
Unit Review

Get started on the
Unit Review problems
in the Collaborate
section...
Ask your questions
in our Unit Discussion.
Learn

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:

