
Unit 1 - Sequences and Series

Statement of Inquiry
Number and algebra allow us to represent patterns, show equivalencies and make generalizations which enable us to model real-world situations.
Learning Topics
-
Arithmetic and geometric sequences
-
Arithmetic and geometric series
-
Common difference
-
Sigma notation
-
Common ratio
-
Sum of sequences
-
Binomial Theorem
-
Proof
-
Sum to Infinity
Prior Learning Support
Prior Learning Topic 1 - Solving Linear Equations
Prior Learning Topic 2 - Fractions
Prior Learning Topic 3 - Order of Operations
Prior Learning Topic 4 - Substituting in Formulae
Concepts
Patterns, Generalization
Patterns: Sets of numbers or objects that follow a specific pattern or rule.
READ MORE >
Generalization: A general statement made on the basis of specific examples.
READ MORE >
Course Syllabus Topics

Conceptual Understandings
-
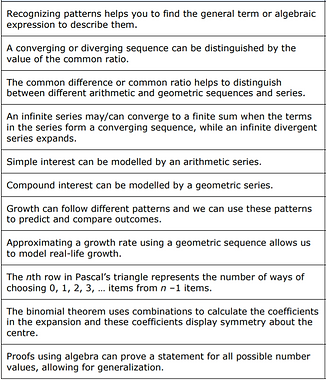
Modelling real life situations with the structure of arithmetic and geometric sequences and series allows for prediction, analysis and interpretation.
-
Patterns in numbers inform the development of algebraic tools that can be applied to find unknowns.
-
The binomial theorem is a generalization that provides an efficient method for expanding binomial expressions.
Further Conceptual Understandings
Unit Discussion
Questions & Suggestions
Click on the microphone icon to enter our Unit and Lesson Discussion.
-
Begin a discussion thread by adding a specific question under a Lesson heading.
-
Suggest links to videos and websites that have helped you in your learning.
Lesson 1:
Patterns and
Sigma Notation
Link to the Course Calendar

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Do the names that we give things impact how we understand them?
Who would you call the founder of algebra?
Is mathematics a language?
Reflect
Lesson 2:
Arithmetic
Sequences

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Is all knowledge concerned with identification and use of patterns?
Reflect
Lesson 3:
Geometric
Sequences

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
How is intuition used in mathematics?
Reflect
Lesson 4:
Arithmetic and Geometric Series

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Is it possible to know things about which we can have no experience, such as infinity?
Reflect
Lesson 5:
Infinite
Geometric Series

Video Lesson 1
Video Notes Page
Video Lesson 2
Video Notes Page
Ask your questions
in our Unit Discussion.
Learn

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
How do mathematicians reconcile the fact that some conclusions conflict with intuition?
Do all societies view investment and interest in the same way? What is your stance?
Reflect
Lesson 6:
Pascal's Triangle
& Binomial Expansion

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Although Pascal is credited with bringing this triangle to the Western world, it had been known in China as early as the 13th century. What criteria should be used to determine who "invented" a mathematical discovery?
Are mathematical theories merely the collective opinions of different mathematicians, or do such theories give us genuine knowledge of the real world?
How many different tickets are available in a lottery? What ethical considerations are there?
Reflect
Lesson 7:
More on
Binomial Expansion
Lesson 8:
Unit Review

Video Lesson - Proofs
Video Lesson 2
- Binomial Challenge
Short Practice
Ask your questions
in our Unit Discussion.
Learn

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
Mathematics may be defined as the economy of counting. There is no problem in the whole of mathematics which cannot be solved by direct counting. E.Mach. Agree or disagree?
What is the role of the mathematical community in determining the validity of a mathematical proof?
Reflect

In SeeSaw, respond to one. Then, comment to someone else with agreements/disagreements.
TOK Reflections:
None today.

